Index-free Adjacency Explained

グラフデータベースの内部実装について理解しようとすると、"Index-free Adjacency" という言葉に出くわすことでしょう。

例えば、「グラフネイティブな実装がされたグラフデータベースでは、Index-free Adjacency のおかげで高いクエリパフォーマンスを実現することができる」 といった文脈で紹介されることが多いです。

今回は、この Index-free Adjacency について紹介します。

インデックスとは何か

そもそも、リレーショナル・データベース（以下：RDBMS）におけるインデックスとは何かについておさらいしてみましょう。

インデックスとは、「索引」のこと。データベースへ特定のデータを問い合わせるにあたって、事前に索引集を作っておくことで、ほしいデータにすばやくアクセスできるようにするものです。

具体例：RDBMS - インデックスを使わない場合

SNS アプリにおいて、「ユーザー "Alice" がフォローしている他のユーザー」をデータベースから問い合わせるケースについて考えてみましょう。

RDBMS を用いてデータモデリングをしてみましょう。ただし、最初の例ではインデックスを使わないケースについて考えています。

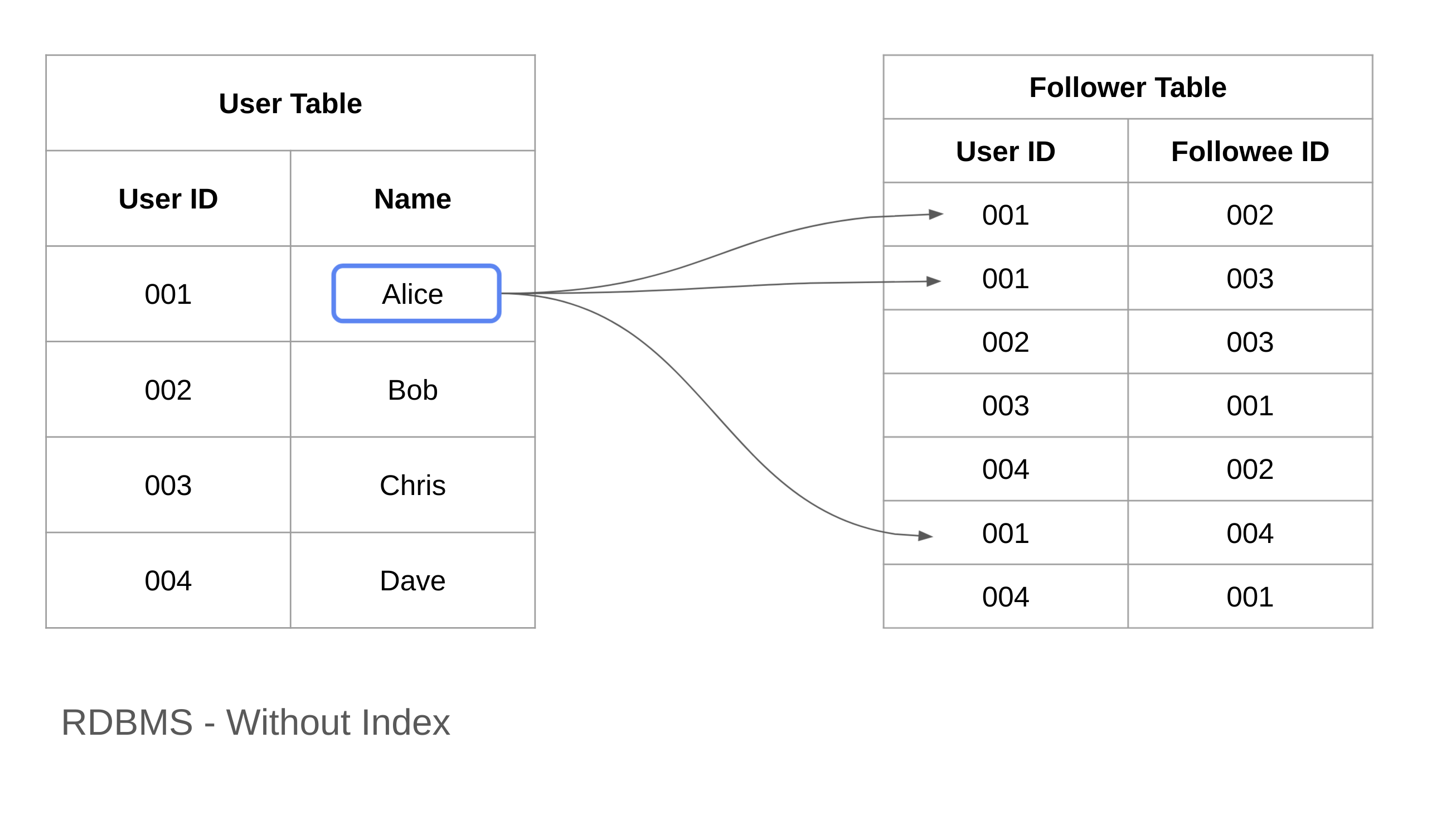
以下の図のように、User テーブルにユーザー情報を格納します。そして、どのユーザーが誰をフォローしているかを表現するために、Follower テーブルを作成してみましょう。

例えば Alice (User ID = 1) のフォローしているユーザーを探索するとき、Follower テーブルから User ID == 1 の行を探すことになります。

テーブルのどの行に入っているかはわからないので、一行目から総当りで見ていく必要があります。

したがって、このとき Follower テーブルの行数を N としたとき、探索コストは O(N) となります。データ量に対して線形に探索コストが増えてきます。

具体例：RDBMS - インデックスを使う場合

次に、索引表を利用するケースを考えてみましょう。

索引表とは、特定の項目が辞書のどのページに記載されているかを確認するキー・バリュー型のリストです。

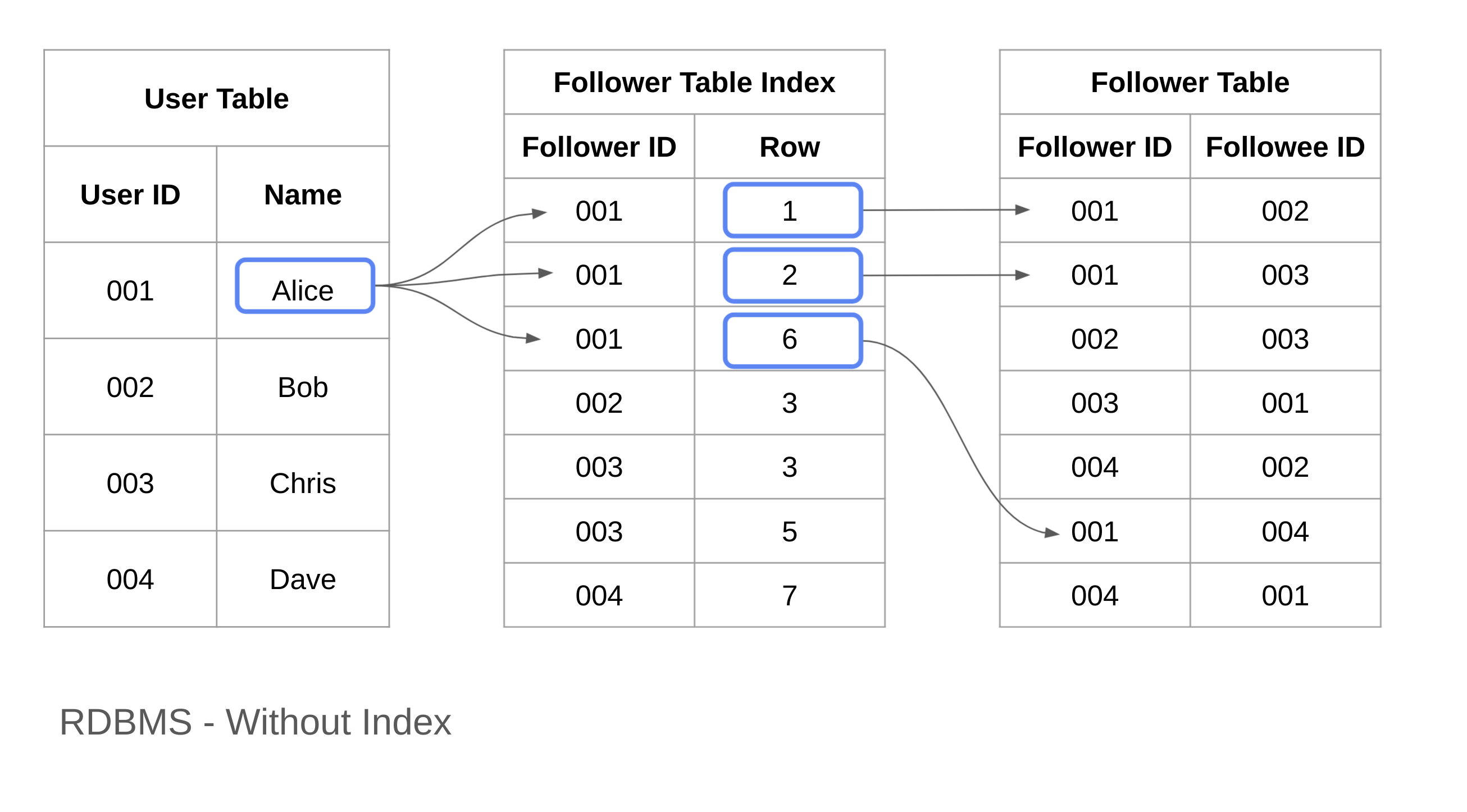
例えば、ここでは「Followr ID」から「行番号 (Row Number)」を引く Follower Table Index を作成するとします。

Hash<K, V> = <Int, Int>
K = Follower ID
V = Row Number

インデックスに問い合わせるとき、インデックスのデータ構造を何で実装するか次第で探索コストは変わりますが、O(log(N)) となることが多いです。

そして、インデックステーブルには Follower Table の行番号が記載されているので、O(1) で引けます。

したがって、インデックスを利用した場合の探索コストは、O(log(N)) となります。

インデックスの欠点

ここで、索引集を「運用」するケースについて考えてみます。

辞書の改訂版を出版するとします。新しい単語を追加したり、古い単語を削除したりすることで、ページ数が大きく変わります。

このとき、辞書巻末にある索引集については、どうなるでしょうか？... ご想像の通り、ページ数を更新しなくてはなりません よね。

RDBMS について考えてみましょう。作成済みのインデックスというのは、物理的にはディスク上に保存されたデータベース本体とは別の物理ファイル に過ぎません。

索引集を考えてみてもそうです。辞書本体とは別で余分に紙面を利用した追加のリスト、ですよね。データベース本体に更新が走った場合、インデックスも同時に更新してあげなくてはなりません。

したがって、インデックスを作成するということは、追加で書き込み時のパフォーマンス低下、および余分なディスク容量を利用する というトレードオフを抱えているのです。

問い合わせのクエリ速度向上とのトレードオフです。現代のアプリケーションでは書き込みより読み込みの方が多いケースが多いので、大抵の場合インデックスを作るという選択をしたほうが割に合うのですが、書き込みのほうが多いアプリケーションでインデックスを必ずしも作るべきではないのは、これが理由です。

具体例：グラフデータベースの場合

グラフネイティブなグラフデータベース、すなわち Index-free adjacency を達成しているグラフデータベースでは、全てのデータは関係性をディスク上で表現しています。

例えば Neo4j の場合、ノードと呼ばれるデータを表現するオブジェクトは、リレーションと呼ばれる関連性を表現するオブジェクトの ID を参照として持っています。要するに、ポインタです。

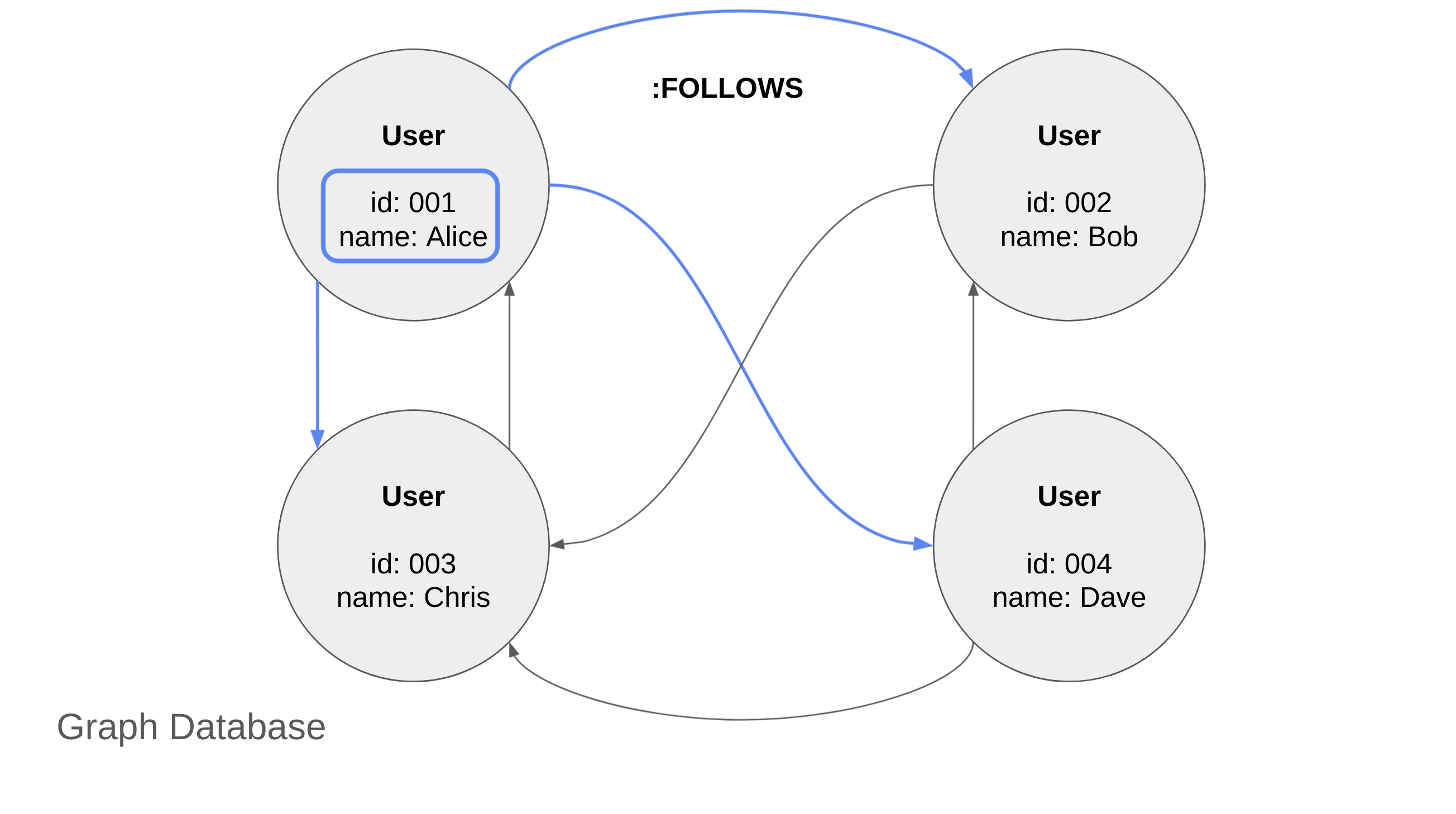
関連性のあるデータ同士は、ポインタを通じて直接ディスク上で隣同士であることが表現されています。グラフデータベースの世界では、データのことと「ノード」、ノード間のつながりのことを「リレーション」と呼んでいます。

Index-free adjacency とは、直訳すると「インデクス不要な近接性」。言い換えると、インデックスがなくても関連するノード同士が近くにある データ構造と言えるでしょう。

したがって、関連するノード同士の問い合わせは常に O(1) となります。

例えば、「ユーザー "Alice" がフォローしている他のユーザー」のノードは、Alice ノードから全て１ステップでたどり着くことができます。

これが、Index-free adjacency であるグラフデータベースで、問い合わせクエリが O(1) を達成できる理由です。

最後に

以上、Index-free adjacency について、RDBMS のインデックスと比較しながら説明してきました。